Derive the equations of motion for the system

Derive the equations of motion for the system

Mechanical Engineering

Consider the mass M subject to periodic forcing P(t) = P sin ωt + ε sin ω₂t, where ε is a small parameter. The mass is attached to a spring with stiffness k and dashpot with damping coefficient c to model the stiffness and damping of the structure. Resting atop the idealized structure is vibration damper consisting of a mass ma, spring ka, and dashpot ca. as shown in Figure. The goal is to make the appropriate choice of the parameters m_a, k_a, c_a to minimize the oscillations of the main structure. For consistency, make use of the following notation;

ω_a = √(k_a/m_a), ω_π = √(k/M) and β = ω/ω_π, β2 = ω₂/ω_π

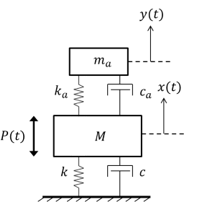
Figure – Schematic diagram of the idealized model for the mass M and vibration absorber.

Questions-

1. Derive the equations of motion for the system.

2. Derive the associated transfer functions.

3. CASE I: Consider the special case with c_a = 0. Let M = 1kg, c = 3N/(m/s), k = 2 N/m, m_a = 0.05kg and ω₁ = 1, ω₂ = 0 rad/s. How will you choose Ica to completely eliminate the oscillations of the structure?

4. CASE II: Add damping c_a = 0.3N/(m/s) to the vibration absorber in CASE I. What happens when i) ω_a = 0.5 ω_n, ii) ω_a = ω_n, iii) ω_a = 2ω_n?

5. CASE III: Let ε/P = 0.01 be a small number. This corresponds to the case where the external force has a small perturbation with frequency ω₂. How does the inclusion of this force affect the design of your vibration damper in CASES I and II?